Author Archives: Mr. Chase

Women & Math

Posted on by
2

Here’s a thoughtful TED talk from Laura Overdeck of bedtime math. I’ve highlighted this website before and I think it’s such a brilliant idea for kids! Laura was the lone girl in her astrophysics undergraduate studies, so she has a great vantage point from which to give this stellar talk (pun intended! 🙂 ).

She has lots of great points. In particular, I liked these three simple recommendations for women–and for everyone:

  1. Don’t play the lottery.
  2. Don’t say you hate math.
  3. Don’t ask others to calculate the tip.

 

Improper integrals debate

Posted on by
1

Here’s a simple Calc 1 problem:

Evaluate  \int_{-1}^1 \frac{1}{x}dx

Before you read any of my own commentary, what do you think? Does this integral converge or diverge?

image from illuminations.nctm.org

Many textbooks would say that it diverges, and I claim this is true as well. But where’s the error in this work?

\int_{-1}^1 \frac{1}{x}dx = \lim_{a\to 0^+}\left[\int_{-1}^{-a}\frac{1}{x}dx+\int_a^{1}\frac{1}{x}dx\right]

= \lim_{a\to 0^+}\left[\ln(a)-\ln(a)\right]=\boxed{0}

Did you catch any shady math? Here’s another equally wrong way of doing it:

\int_{-1}^1 \frac{1}{x}dx = \lim_{a\to 0^+}\left[\int_{-1}^{-a}\frac{1}{x}dx+\int_{2a}^{1}\frac{1}{x}dx\right]

= \lim_{a\to 0^+}\left[\ln(a)-\ln(2a)\right]=\boxed{\ln{\frac{1}{2}}}

This isn’t any more shady than the last example. The change in the bottom limit of integration in the second piece of the integral from a to 2a is not a problem, since 2a approaches zero if a does. So why do we get two values that disagree? (In fact, we could concoct an example that evaluates to ANY number you like.)

Okay, finally, here’s the “correct” work:

\int_{-1}^1 \frac{1}{x}dx = \lim_{a\to 0^-}\left[\int_{-1}^{a}\frac{1}{x}dx\right]+\lim_{b\to 0^+}\left[\int_b^{1}\frac{1}{x}dx\right]

= \lim_{a\to 0^-}\left[\ln|a|\right]+\lim_{b\to 0^+}\left[-\ln|b|\right]

But notice that we can’t actually resolve this last expression, since the first limit is \infty and the second is -\infty and the overall expression has the indeterminate form \infty - \infty. In our very first approach, we assumed the limit variables a and b were the same. In the second approach, we let 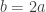b=2a. But one assumption isn’t necessarily better than another. So we claim the integral diverges.

All that being said, we still intuitively feel like this integral should have the value 0 rather than something else like \ln\frac{1}{2}. For goodness sake, it’s symmetric about the origin!

In fact, that intuition is formalized by Cauchy in what is called the “Cauchy Principal Value,” which for this integral, is 0. [my above example is stolen from this wikipedia article as well]

I’ve been debating about this with my math teacher colleague, Matt Davis, and I’m not sure we’ve come to a satisfying conclusion. Here’s an example we were considering:

If you were to color in under the infinite graph of 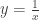y=\frac{1}{x} between -1 and 1, and then throw darts at  the graph uniformly, wouldn’t you bet on there being an equal number of darts to the left and right of the y-axis?

Don’t you feel that way too?

(Now there might be another post entirely about measure-theoretic probability!)

What do you think? Anyone want to weigh in? And what should we tell high school students?

.

**For a more in depth treatment of the problem, including a discussion of the construction of Reimann sums, visit this nice thread on physicsforums.com.

Lego Price Statistics

Posted on by
1

Do you ever get the feeling that Lego Bricks are becoming more expensive? When we were kids, boy, it felt like they were cheaper, right? I mean, the biggest sets were $150 at most. I have a HUGE Lego collection, and it definitely seems like Legos back in my day were more affordable.

Trouble is, that’s not really true. It turns out that Lego bricks have actually gotten cheaper, by almost every measure you can think of (weight/number of pieces/licensed sets). Check out this incredibly thorough post on Lego Price statistics over time. The article is entitled, “What Happened with LEGO” by Andrew Sielen. It’s very thoughtfully done.

[ht: Gene Chase]

Half-your-age-plus-seven rule

Posted on by
3

Looking for a great application of systems of linear inequalities for your Algebra 1 or 2 class? Look no further than today’s GraphJam contribution:

You might just give this picture to students and ask THEM to come up with the equations of the three lines.

There’s also a nice discussion to be had here about inverse functions, or about intersecting lines. And there might also be a good discussion about the domain of reasonableness.

Here are the three functions:

f_{\text{blue}}(x)=x

f_{\text{red}}(x)=\frac{1}{2}x+7

f_{\text{black}}(x)=2x-14

This is especially interesting because I never think of the rule as putting boundaries on a person’s dating age range. Usually people talk about it in the context of “how old of a person can I date?” not “how young of a person can I date?” Or rather, if you’re asking the second question, it’s usually phrased “how young of a person can date me?” (All of these questions relate to functions and their inverses!) But in fact, the half-your-age-plus-seven rule puts a lower and and upper bound on the ages of those you can date.

As far as reasonableness, is it fair to say that my daughter who is 1 can date someone who is between the age of -12 and 7.5? I don’t think so! I’m definitely going to be chasing off those -12 year-olds, I can already tell :-).

For my daughter, the domain of reasonableness might be x\geq 18!

Happy e day!

Posted on by
2

Well, as you can see by the count-down on the right side of this blog, e day has arrived! I mentioned it in most of my classes today, even though it’s not as well-celebrated as π. I think we should change that. It’s my opinion that e is at least as good, if not a more important constant, than π.

I’m biased though. Today is also my daughter’s first birthday. I love that she was born on e day! Awesome! 🙂

hand

Happy Birthday, Ruthie Chase!

 

Friday tidbits

Posted on by
Reply

Happy Friday! Hope everyone has their kids registered for the AMC next week. If you haven’t already subscribed to the AMC problem-a-day from the MAA, you should! It’ll keep you sharp :-).

Here are a few nice things seen ’round the web recently:

  • The Scrambler, by Dan Meyer & co. Here, Dan challenges us to analyze a classic carnival ride, and asks us to predict where you end up at the end of the ride. And by Dan & “co”, I mean “comment” folks who have generated lots of fun solutions and applets. Dan made a great interactive version here, too.

  • And finally, this lengthy article “Reflections on mathematics and Democracy” by Lynn Arthur Steen is well worth the time [ht: Gene Chase]. He thoughtfully discusses the need for math education among the citizenship. Is “usefulness” to the democracy the highest goal of secondary math education? Do we aim to create quantitatively literate citizens? Or do we put them on the Calculus track and prepare them for college-level STEM careers? Does teaching “quantitative literacy” even count as Mathematics with a capital M? This is obviously something I’ve been thinking a lot about recently. Here are a few of my favorite excerpts:

Ten years ago I addressed the first question posed to this panel in Mathematics and Democracy—a collection of essays from a variety of professionals both inside and outside mathematics.4 (These essays are available for free downloading on the MAA website.) The chief message of this volume is that the mathematics taught in school bears little relationship to the mathematics needed for active citizenship. That mathematics we called quantitative literacy (QL) to contrast it with traditional school mathematics which, historically, is the mathematics students needed to prepare for calculus.

Mathematics and quantitative literacy are distinct but overlapping domains. Whereas mathematics’ power derives from its generality and abstraction, QL is anchored in specific contexts and real world data. An alternative framing of the challenge for this panel is to ask whether perhaps QL might be a more effective approach to high school mathematics for all.

…

What we forget, however, is that when NCTM initiated its standards work, most mathematics teachers did not actually believe in the goal of teaching mathematics to all high school students. Whereas now we argue about how much and what kind of mathematics to teach in high school, three decades ago debate centered on who should learn high school mathematics. At that time, the curriculum was designed to efficiently sort students into those who were capable of learning high school mathematics and those who were not. So between grades 7 and 9, somewhere between one-third and one-half of the students were placed in a course called General Math—an enervating, pointless review of arithmetic.

…

Another decade has passed, and our ambitions are now much higher: a common core for all, with everyone emerging from high school ready for college. In one generation, the political view of high school mathematics has progressed from something only some need (or can) learn to a core subject in which all students can and must become proficient. That’s quite a rapid change in ends, which has been matched by a major change in means. The very idea of a common curriculum enforced with common assessments was all but unthinkable back in the 1980s.

Math is not linear

Posted on by
3

This presentation has been around for a few years, but I’ve never highlighted it here on my blog. It’s a Prezi presentation by Alison Blank and it’s called Math is not linear.

It brings up an excellent point that math is often talked about as being a sequence with one class coming before another, when in fact math isn’t always like this. It is absolutely true that there’s room for prerequisites (it’s not a great idea to take Calculus 3 before Calculus 1), but much of mathematics can be approached at any time.

math courses–perhaps more like a tree then a line?

Math majors realize this when they get to college. Once you take a few basic classes like Calculus, Linear Algebra, and Statistics, you can take almost any other course you want. Occasionally there are other prerequisites (a two-course sequence in Differential Equations might require students to take them in order). But generally, you can order your college math courses in many different ways.

I’ve noticed this in grad school too. Here’s the order I’ve taken my classes so far with my comments:

  1. Differential Equations (took it in undergrad too, which helped!)
  2. Cryptography (might have been good to do abstract algebra first, but we learned the practical things we needed to know along the way)
  3. Abstract Algebra (when we talked about cryptography and elliptic curves, it was total review!)
  4. Real Analysis (took it in undergrad, but boy I understood it a lot better the second time around)
  5. Statistics (took it in undergrad, but I loved learning it from a more theoretical, Calculus-based approach)
  6. Queueing Theory (stat required, for good reason; just started this course, so I can’t tell you much more)

Did I have to take these courses in this order? Not necessarily. I’ve found that cross-references are made between courses constantly. In my queuing theory class this past week, we solved a differential equation. So there! 🙂

Could we do this in high school? To some extent, yes. I think it’s still important to have prerequisites, however. And to get to Calculus, you have to take a *somewhat* linear path. (Do you agree that Calculus is the pinnacle of high school mathematics?) Along the way, though, we should indulge in lots of mathematical tangents, as the Prezi suggests.

In some ways we already allow our students a bit of latitude. We offer AP Statistics, which can can be taken almost anytime after Algebra 2. And we offer Higher Level math, which gives a nice taste of college-level math.

As Alison Blank suggests, could we teach a little topology to high school students? Certainly we could. Weren’t we all interested in the advanced math topics before we actually took the class? I remember learning all the fun and interesting results from topology way before I ever read through a topology textbook. I still haven’t taken a class in topology! (But I read a lot of Munkre’s book and did a lot of the exercises, and I think that counts for something :-).)

The point is, I think we can talk about fun and interesting math ideas way before we’re “allowed” to talk about them!

That’s certainly what my dad did with me at home. Thanks dad!

I dedicate this post to all those math teachers who went on a mathematical tangent this week. Keep up the great work!