Category Archives: Uncategorized

Geometric Proofs of Trigonometric Identities

Posted on by
4

Sparked by a conversation this past weekend about the usefulness of the half-angle identities, I constructed geometric proofs for \sin(x/2) and \cos(x/2). Since I’ve never seen these anywhere before, I thought I’d share.

And while I was at it, I thought I’d share all my other geometric proofs, so here they are, posted mostly without comment.

Some of these are so well-known as to be not worth mentioning. Many of them have been stolen from Proofs Without Words I or Proofs Without Words II. I came up with a few of them myself. Frustratingly, almost none of them are to be found in Precalculus textbooks, where they might be learned and appreciated.

Pythag 1

________________________________________________________

Pythag 2

__________________________________________________________

Pythag 3

_____________________________________________________________

Pythag 4

________________________________________________________________

Sincos of a sum 1

_______________________________________________________________Sincos of a sum 2

______________________________________________________________

sincos of a diff 1

_________________________________________________________________

sincos of a diff 2

______________________________________________________________

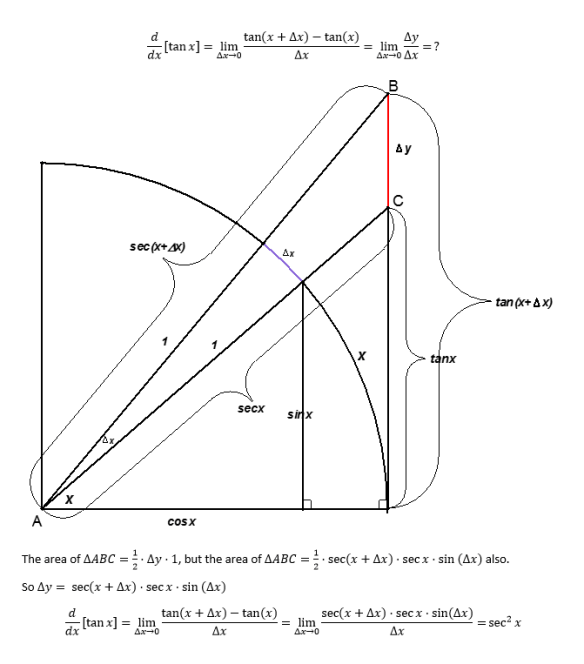
Though this one is my favorite:

sine and cosine of a sum best 1

____________________________________________________________________________

sine and cosine of a sum best 2

_______________________________________________________________________________________

Partially because of the way it naturally generalizes into the proof of the derivative of sine. If you just let \beta approach 0, \cos(\beta) approaches 1 and that point in the interior of the circle ends up on the circle, where \sin(\beta) merges with \beta itself.

Proof of derivative of sinx

_____________________________________________________________________________________

double angle 1

______________________________________________________________________________________

double angle 2

_______________________________________________________________________________________

double angle 3

___________________________________________________________________________________

half angle 1

__________________________________________________________________________________

half angle 2

___________________________________________________________________________________________

half angle 3

____________________________________________________________________________________

 

half angle 4____________________________________________________________________________________

And finally, one that shows that the sum of a sine and cosine function of the same argument is also a sinusoid. Since I lost the original picture and don’t feel like remaking it, you’ll have to complete the proof on your own!

sum of sine and cosine

____________________________________________________________________________________

Update: After some feedback on twitter, I’ve decided to add a few more diagrams. Tim Brzezinski sent me a link to his website of geometric proofs of trig identities and he had some that I’ve never seen before.

Check it out!

https://www.geogebra.org/m/DxAcj8E2#material/QedMT7Pw

I’ve taken two of his diagrams and added them below.

tan of a sum 1

_________________________________________________________

tan of a sum 2

____________________________________________________________________________________

tan of a diff 1

_________________________________________________________________________________________

tan of a diff 2

Derivatives of Trigonometric Functions

Posted on by
13

First, let’s present the standard approach. This is from the calculus textbook I teach out of.

der of sinx

This was, as far as I was concerned, the only possible proof. The pedagogical flexibility lay entirely in how to frame the question, how to get students to discover the fact on their own (via graphical techniques), and how to add extra meaning to the result.

The most important question, so I thought for years, was really how one introduces and understands the fact that \lim_{x \to 0} \frac{\sin x}{x}=1. Some textbooks introduce it more or less out of the blue as “an important limit to know” and prove it via the Squeeze Theorem. Others prefer to wait until halfway through the above proof, realizing only then that this limit is important and solving it with a purpose in mind. There is also a difference of opinion as to how much rigor is required to establish the key inequality, that \sin \theta < \theta < \tan \theta. My textbook uses an area argument, but others prove the inequality with a nested sequence of segment inequalities.

My personal preference is for students to encounter \lim_{x \to 0} \frac{\sin x}{x}=1 “naturally” by attempting to graph y=\frac{\sin x}{x} in precalculus, along with other interesting functions like y=x \cdot \sin x, y=x \cdot \cos x, y = x + \sin x, y = e^{-x} \cdot \sin x, and y = \sin(1/x). These are more or less exercises in recognizing the so-called “envelope” of the product or sum of a periodic function and another function and have various scientific applications. The very informal geometric argument for why \lim_{x \to 0} \frac{\sin x}{x}=1 that one encounters in precalc prepares one for the more formal proof in calculus via the Squeeze Theorem.

All of this hard work to prove that \lim_{x \to 0} \frac{\sin x}{x}=1 almost seems to make it the real theorem and leaves \frac{d}{dx} [\sin x] = \cos x as a corollary.

By contrast, consider this:

Proof of derivative of sinx

I’m tempted to make no further comment, since this beautiful and striking diagram so thoroughly and clearly explains why the derivative of sine is cosine. Tiny changes in the sine of an angle are proportional to the cosine of that angle since the red arc length above is effectively a tangent to the circle. I would go so far as to say that until you see a diagram like this, you don’t even really understand the theorem at all. Why don’t we teach the derivative of sine this way? Why is this figure not in all the textbooks? I think I know the answers to these questions. The answers involve a long story about the history of calculus, the banishment of infinitesimals during the quest for rigor, and the abandonment of geometry as a satisfactory basis for analysis. But these diagrams are just too beautiful to give up and it’s cruel of us to keep them hidden from our students.

Here’s another calculus proof:

Proof of derivative of arcsinx

Compare this to the standard treatment you find in textbooks:

crapderarcsine

Which one of these proofs excites you? Which one makes you really feel like you understand the theorem and why it’s true?

I have created an entire series and I post them here without further comment.

Proof of derivative of tanx

Proof of derivative of arctanx

Proof of derivative of secx

Proof of derivative of arcsecx

 

Matthew Wright visits RM

Posted on by
2

Dr. Matthew Wright paid our students a visit this past Friday and gave them a gentle introduction to topology and the Euler Characteristic. This is a topic given little to no treatment inside the traditional K-12 math curriculum, so our students welcomed the opportunity to learn some ‘college math.’ IMG_20140404_111835821He had our students counting vertices, edges, and faces of various surfaces in order to compute the Euler Characteristic. Students discovered that the Euler Characteristic is a topological invariant.

IMG_20140404_111817820In his talk he also walked the students through a proof that there are only five regular surfaces, using the Euler Characteristic. This is more difficult than the typical proof, but elegant because the proof doesn’t appeal to geometry. That is, the proof doesn’t ever require the assumption that the faces, angles, or edges are congruent. In this sense, it is a topological proof.* Very cool indeed!

Matthew's topology guest lecture at RMHSBio: Matthew Wright went to Messiah College and then went on to received his MS and PhD from University of Pennsylvania, where his thesis was in applied and computational topology. He was a professor at Huntington College for two years but is now at the Institute for Mathematics and its Applications at the University of Minnesota for a postdoctoral research fellowship. His hobbies include photography and juggling. On a personal note, Matthew was my roommate in college, and I had the privilege of being his best man in his wedding, as well!

For more about Dr. Wright, visit his website at http://mrwright.org/.

* This proof also appears in the book Euler’s Gem by Dave Richeson.

Chinese bridge inspired by Möbius band

Posted on by
1

Bridge_04

[Guest post by Dr. Chase]

Is THIS bridge pictured above in the shape of a Möbius band or merely “associated” with a Möbius band as the article suggests?  If it is a Möbius band, where is the half-twist?  Do you think that the bridge is beautiful?  The architects have proposed that such a bridge be built in China.

Can you imagine a Möbius band being used for a road?  There was “A subway named Möbius,” to quote the title of a light-hearted 1950 short story by A. J. Deutsch.  It was published in the wonderful 1958 book Fantastia Mathematica.

The bridge above is only a concept.  Other one-sided surfaces have inspired architectural designs that have actually been built.  Here’s a house made in the shape of a Klein bottle.

A bit of mathematical humor.  One person comments on the Klein bottle that he likes the house’s orientation.  Well, if it were a true Klein bottle, it wouldn’t be orientable at all!