I mentioned the A4 paper size (European standard) today in some of my classes and its special 
ratio. It has the amazing property that if you cut it in half “hamburger” style it retains the ratio. Incredible, right? Beautiful, right? Nothing special about our 8.5″ x 11″ paper, that’s for sure. For extra bonus points, give a proof of this property (it’s two or three statements–short and simple).
Elegantly, A0 paper is proportioned so that it has exactly 1 square meter of area. A1 is half that size, A2 half again, and so on. For more info about A4 paper, and diagrams, visit the Wikipedia page.
Like this:
Like Loading...
Related
Random Walks 
Proof (I admit Wikipedia helped a bit):
“sq2” means “square root of 2”.
Assume a rectangle of dimensions x and y, where x = y * sq2, and x and y are integers. The aspect ratio will be the quotient of longer and shorter side, x / y, which simplifies to (y * sq2) / y or sq2. Cut the rectangle in half so that y is now the longer side, and the shorter side measures x / 2. Now, the aspect ratio is y / (x / 2), so x / y = y / (x / 2). Simplify. x^2 / 2y = y. x^2 / 2 * y^2 = 1. x^2 / y^2 = 2. x / y = sq2. QED
Nice! I knew I could count on you, Drew :-). Now you just need to learn how to tag with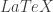
so it looks pretty, like this: 
.